

















Everything in Proportion
If I had my time at primary school over again, I think I would have liked Mr Poultney to be my Maths teacher. Then I would have stood a fighting chance of knowing what I was doing, and I might even have enjoyed the experience! In my day, Maths amounted to little more than a list of calculations on a page. It didn’t seem important for pupils to talk about what they were doing, still less why they were doing it and what relevance the work would have for life outside the classroom. Only since I have been teaching have I come to appreciate the beauty in Mathematics and to understand that, whilst very often there is only one right answer, there are very many ways of arriving at that answer. This creativity and flexibility of thinking lies at the heart of Mr Poultney’s approach to Maths.
Quite early on in his lesson with Form 6 this week, Mr Poultney produced a diagram of Bloom’s Taxonomy. This little diagram, which you can see illustrated above, has become part of teachers’ DNA, and illustrates the developing complexity of learning objectives. Mr Poultney related this directly to the learning experiences of his group. At the start, he said, there is knowledge, pure and simple, but to go further and make sense of what you are learning, you have to have comprehension. Once you have this, you are in a position to apply what you have learnt.
This is especially pertinent for Form 6 children, who are currently sitting their 11+ examinations. As a teacher, when preparing children for exams, you might have sheaf upon sheaf of past papers, but you cannot know exactly what is going to come up in a particular year or what angle the question will take. It falls to the children themselves to filter the information and apply what they have been taught in school.
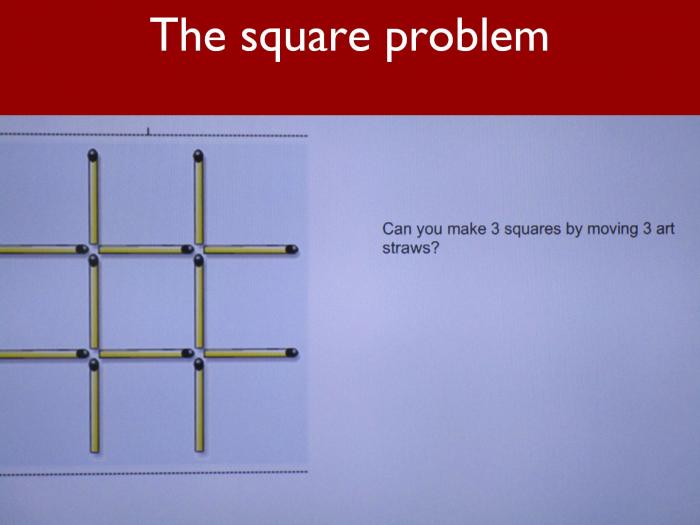
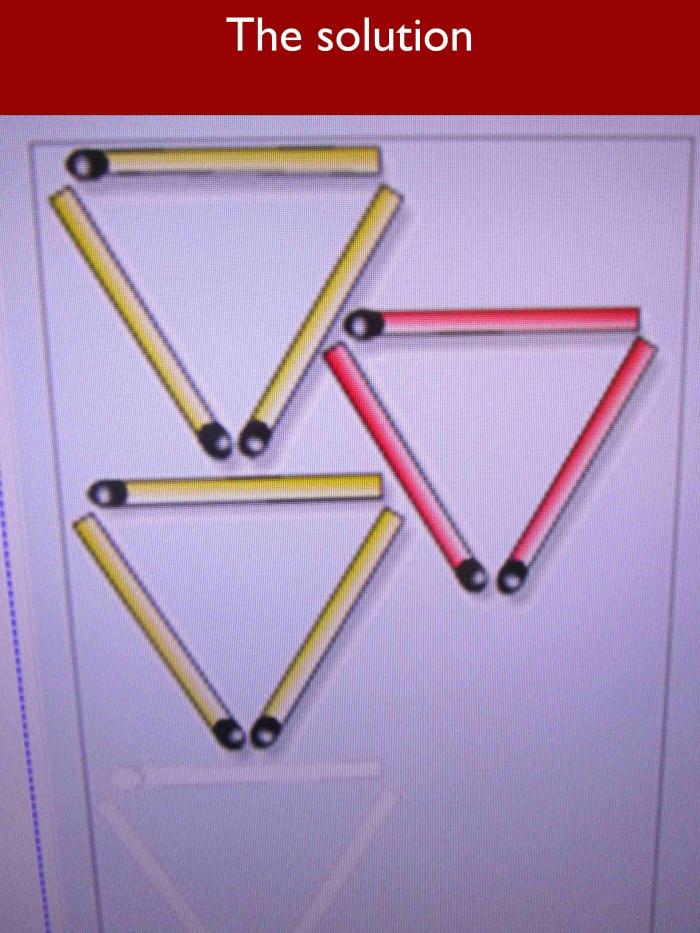
Mr Poultney’s starter activity was just the sort of challenge that might emerge from the left field on an examination paper. He fetched out a larger drawer of cut down art straws and asked the group to solve a problem involving squares, reminding the children of the importance of being resilient and of trying different methods if initially they were unsuccessful. Working with a partner, most of the children solved the puzzle, although not before they were caught out moving too many straws or failing to create enough squares. The triangle puzzle was craftier and, despite some valiant attempts and a couple of clues provided by Mr Poultney, it didn’t find a solution until it was demonstrated on the board.
Unsurprisingly, this focus for Form 6 this half term is revision and, in order to use precious lesson time most effectively, Mr Poultney asked the children to suggest priority areas for further study. Nothing would be gained, he told them, from trundling through areas such as place value or column addition, where they already feel confident, just because the curriculum says so. Far better to concentrate on a topic where the children are less secure, and from this they identified ratio.
Ratio and proportion do not appear on the curriculum further down the school, although they are alluded to in practical contexts such as Food Technology or when looking at patterns in calculations, such as relating 2 +3 = 5 to 20 + 30 = 50. When Mr Poultney asked the children to define ratio, he got some thoughtful answers, and it quickly became apparent how closely related this area of learning is to the more familiar fractions and division. The key thing to remember, he said, is that ratio is a way of comparing different values, or alternatively as a means of dividing a quantity into unequal shares.
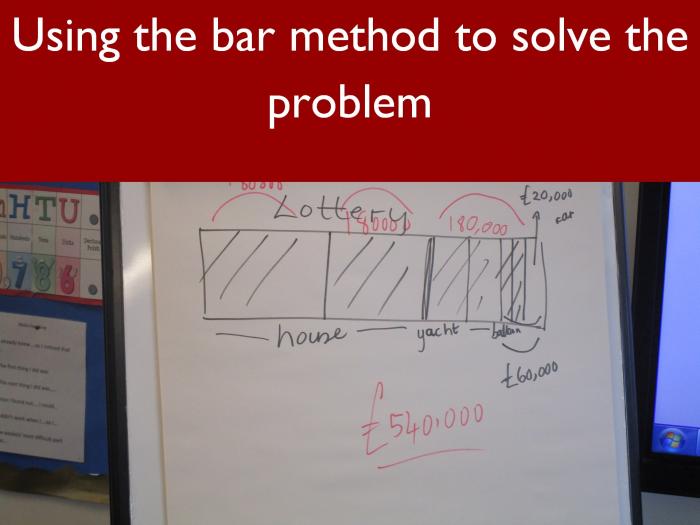
Ultimately, Mr Poultney’s aim was to arm the children with practical strategies to use in examinations but, to start with, and with no preamble, he posed them a problem about Slick Jim and his apparent squandering of his lottery winnings, and asked them to solve it. Impressively, the children knew instinctively to turn the problem on its head and to start from what they knew, namely that Jim spent his last £20,000 on a luxury car. Working backwards, and multiplying in stages, it was possible to arrive at a total winning jackpot of £540,000. Idina’s cake mixture problem could be solved in a similar way, by judicious use of known facts and also by looking for links and patterns in the numbers.
However, Mr Poultney wanted the children to think about the problems in another way, using the bar method. This is a means of visualising a problem and can be a lifeline when an obvious pattern or route through fails to spring out of a problem. He made it very clear that the use of the bar method was one of his key success criteria, by which he would judge the pupils’ progress in the lesson.
Offering the real life example of paint mixing by proportion at B & Q to show the relevance of ratio, Mr Poultney launched into some more problems. The first involved the ratio of fibre to protein in cereal bars and, although the numbers initially appeared quite unfriendly, the children were able to make sense of it using the bar method. This will make more sense once you have looked at the diagram above!
The second problem, involving the ratio of boys to girls in a sports club, marked the point at which I, as an observer in the lesson, moved from being a teacher to being a pupil. For me, this seemed to be a problem without an obvious starting point. In fact, I would have said there was a fact missing, but drawing the bar model gave it a new dimension and provided a pathway to a solution. Again, please look closely at the diagram above to understand how Mr Poultney made the working so accessible.
As the bell rang for the end of the lesson, I could tell that the pupils were not only reassured by what they had learnt, but they were also enthusiastic and confident, ready to tackle more problems, whether they might come in the next lesson at Eversfield, or when they turn over their examination paper and begin to read the questions.