












Sweet Form 5 and the Awesome Maths Lesson
These days, we are all very aware of the need to reduce the amount of sugar in our diet, but nobody said anything about reducing the amount of sugar in a Maths lesson.
Mr Poultney certainly took his Maths group by surprise the other day when he announced what they were going to do, and the funny thing was that the lesson had started so normally. Out came Jim, Mr Poultney’s faithful pilot teddy bear, whose unlucky fate it is to be flung around the classroom, usually at the expense of his goggles, so the children can answer warm up questions. In this instance, it was halving and doubling numbers with one decimal place. Jim loathes decimals, but he is by nature a helpful bear, so he puts up with the discomfort and is always overjoyed when everyone gets the answers right.
So quick thinking were the children that there was even time for a quick game of Around the World to practise the same objective. Jim was not required for this game, he was relieved to learn, because pairs of children have to go head to head to answer questions posed by Mr Poultney. The child who answers first gets to move around the world, and the other child stays put. The overall winner is the person in the class who travels furthest. Today it was Naomi, who was so hard to beat she almost circumnavigated the globe.
Even at this point in the lesson there didn’t seem to be anything out of the ordinary going on. Mr Poultney reminded the children of the difficulties they had encountered in a recent assessment which enquired about the number of small cubes that make up a larger one. Picking up on errors in tests is something that teachers do all the time, so nothing unusual there. Nor was there when Mr Poultney showed the children a 3 x 3 x 3 cube and asked questions about it.
For example, if someone painted the cube blue, would all the little cubes be blue? Would any be blue all over, on all six faces? Would any not be blue at all?
This is rather troubling, of course, because a cube is not see through, so how is anyone supposed to know? Evie-Mae and Turan thought the cube must be hollow, as indeed is the case with some of the solid shapes we use in school. However this cube, as Mr Poultney pointed out, is entirely made up of small cubes. For Harvey, the notion of counting faces we cannot see was impossible, but Haris thought otherwise. He focused his attention on the cubes in the middle. This, of course, is the core of the problem…but how many cubes are hidden? What happens if we have a 4 x 4 x 4 cube or even a 5 x 5 x 5?
“We can solve the problem,” declared Mr Poultney proudly, “using sugar cubes.” From his bag he produced six boxes of sugar cubes – over 1000 cubes in total – and was immediately deafened by the sound of jaws hitting the floor. The prospect of working with sugar was extremely exciting. This could turn out to be a very memorable lesson, thought the children.
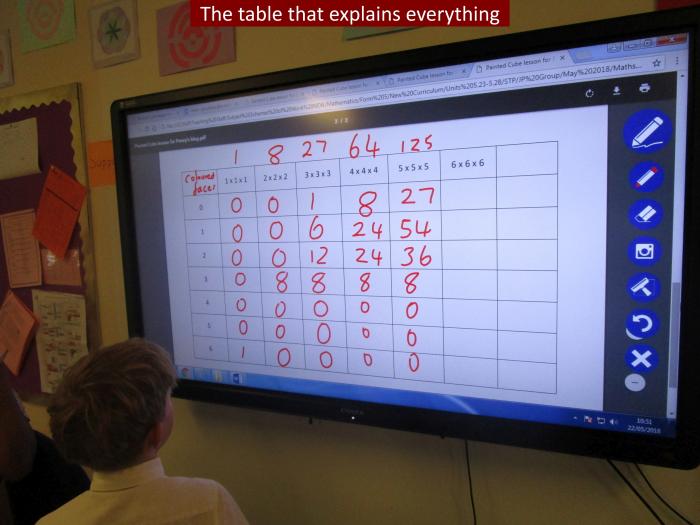
Working with a partner or in a small group, Mr Poultney explained that he wanted the children to build cubes ranging from 1 x 1 x 1 up to 5 x 5 x 5, and beyond if there was time available. They would have to mark the individual cube faces that can be seen when the cube has been constructed, and then count how many of the little cubes have no faces marked, or one face marked, up to a possibility of six faces marked. They would have to record their answers in a table, and I’m pleased to say we have a photograph of the completed table. Readers, you may want to study it carefully before continuing! The children’s excitement was only very slightly dampened when Mr Poultney warned them that on no account were they to eat, or even lick, the sugar cubes!
Inevitably, once the children started investigating, more questions arose, and Mr Poultney took time to clarify the situation. One notable puzzle was whether you should count the cubes on the bottom. After all, when the cubes are sitting on the table, you can’t see them, but of course they are technically on the outside of the cube. Thinking specifically about the 3 x 3 x 3 cube, Mr Poultney wanted to know how many cubes have one face coloured. Lucas thought there would be six, and was able to explain to James that it is the little cube in the centre of the face made up of nine cubes.
As the children completed their grids, Mr Poultney encouraged them to look for patterns. Your blogger always feels reassured when she can find a pattern in anything mathematical, so it was helpful to see that all the constructed cubes, except the 1 x 1 x 1, have eight small cubes where three faces have been coloured. These represent the eight corners of the cube. Equally fascinating was to notice, where two faces have been coloured on the sugar cubes, the 12x table emerging. One would hazard a guess that 48 cubes on the 6 x 6 x 6 construction would have two faces coloured.
However, Mr Poultney wanted the children to look down rather than across the table. If you add the total number of coloured faces for the 3 x 3 x 3 cube, ie. 1 + 6 + 12 + 8, you end up with 27, and that is very significant. Lights pinged on in brains throughout the classroom; 27 is three cubed! Harrison very cleverly realised that this provided a good checking strategy because, if you count the coloured faces and you don’t end up with a cubed number, you must be wrong.
When it was time to pack away, and sweep up all the grains of sugar, Mr Poultney encouraged the children to reflect on what they had learnt. Naomi felt that working practically had helped her visualise the cube more accurately and get a better understanding, particularly about the cubes in the middle that cannot be seen. Everyone was keen to tell the rest of the year group about what fun they had in the lesson, and they were anxious to know when they could do another investigation involving food.
Mr Poultney left the classroom feeling a quiet satisfaction. He was impressed with the way the children had collaborated so successfully, and loved the moment when the penny dropped about the link between the number of coloured cubes and the cubed number itself. Generously, he took his sugar cubes upstairs to the staffroom for the other teachers to use in their break time drinks!